Turns out they were both quite improbable
July 26, 2018 by Aaron Howard in Analysis with 0 comments

July has been quite the month for professional disc golf. Paul McBeth shot what many are calling “The Perfect Round” at the Great Lakes Open, then Eagle McMahon went on to shoot incredible back-to-back 16 under par rounds at the Konopiště Open. After Konopiště, the first question that entered my mind was which feat was more impressive, McBeth’s 18-under round or McMahon’s set of 16-under rounds?
There is a lot to consider when trying to answer this question, so to start I made a plot showing the distribution of scores to par per round for both tournaments. What is clear to me from the plot is that there were many more under par rounds at Konopiště than there were at the GLO. The mean score to par per round at Konopiště was -3.3 and at the GLO it was -2.2.
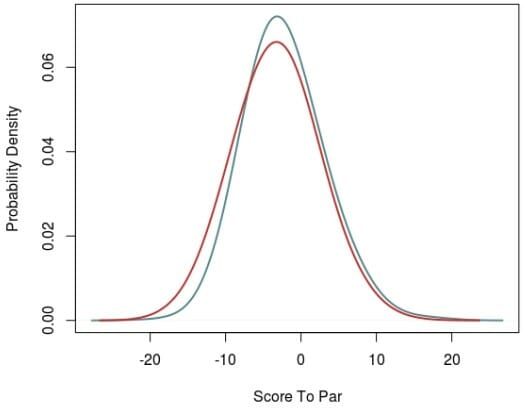
These results may indicate a few important differences about these tournaments.
1. One potential difference is strength of the fields. Perhaps the average score to par was lower at Konopiště because the field was stronger. However, the average ratings of the fields were 978.6 and 980.1, at Konopiště and the GLO, respectively, and are not statistically different from each other.1
2. Another potential difference is scoring difficulty, and by that, I mean how hard is it to score low at each of the two courses. There is a lot that can influence how difficult it is to score low at a tournament (the weather, amount of OB, etc.) but the factor I am going to focus on for this article is the par score.
The importance of par score, in this case, can best be illustrated regarding “The Perfect Round” score of 18-under. If the course has 18 par 3 holes, then the par score is 54 and 18-under is a score of 36. However, if the course is composed of all par 5s, then an 18-under round is a 72. A score of 36 is very different than a score of 72, and they represent very different scoring environments.
For example, on a par 54 course, if an individual is going to go 18 down they must birdie every hole or make up for each missed birdie with an ace. On the par 90 course, if that same individual misses a birdie they can make it up with an eagle.2 What this means is, all else being equal, it should be easier to score 18-under par at a course with a higher par score because it will be easier to “make up for mistake pars.”
Using this logic, I developed what I call a scoring difficulty index that is based on par score. The index equation is:3 For a par 54 course, a score of 36 gives an index value of 1, which is indicative of the fact that one must birdie all of the holes to be 18-under. The difficulty index of a 72 on a par 90 course is 0.6, meaning all else being equal, it is 40% easier to throw an 18-under on a par 90 course than a par 54 course. I plotted “The Perfect Round” index values for course ranging from par 54 through 90 and the values for McBeth’s 18-under and McMahon’s 16-under rounds.
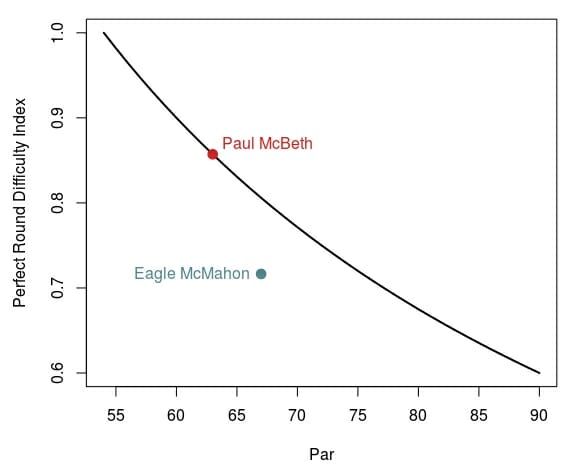
McBeth’s round value is 0.86 and equal to the perfect round score for a par 63 course like the Toboggan. McMahon’s round value was 0.72, which is lower than McBeth’s value and lower than the 18-under value of 0.80 for the Franz Ferdinand course. These values indicate that a single 16-under round on the Franz Ferdinand course is not as impressive as an 18-under at the Toboggan course, and even if McMahon had an 18-under round it would not have been as impressive as McBeth’s 18-under. Again, this is because the scoring difficulty index at the Toboggan was higher than the index at Franz Ferdinand.
So one 18-under at the Toboggan is better than one 16-under at Franz Ferdinand, but we still haven’t answered the main question of the article: are back-to-back 16-unders more impressive than one 18-under? To do this I will use the data given in the first plot in this article to calculate the probabilities for these rounds.4 The probability of McBeth’s 18-under round was 0.0005, and the probability of one 16-under round at Konopiště was 0.005, making McBeth’s 18-under round 10x less probable than either of McMahon’s single 16-under rounds. However, the probability of McMahon’s back-to-back 16-under rounds was 0.00002. So McMahon’s back-to-back was the more improbable feat, using this method, and ultimately more impressive.
You may be thinking, and rightfully so, that I am comparing apples and oranges because I am comparing one round to two rounds. So, I also calculated the probabilities for McBeth’s three rounds (11-under, 18-under, 11-under) at the GLO and McMahon’s first three rounds (16-under, 16-under, 14-under) at Konopiště. McBeth’s probability was 5.2×10-7 and McMahon’s probability was 3.6×10-7. Yes, these numbers are very small (10-7 is seven zeros to the right of the decimal and is a little smaller than the size of a bacteria cell in inches), and yes they mean both of these guys played very well. They also mean that McMahon’s three rounds were more impressive than McBeth’s rounds, but not by that much. This is because, given the par scores, McMahon had more opportunities to score low.
In sum, both McMahon and McBeth played some incredible golf. For a single round, McBeth’s 18-under outdid any of McMahon’s rounds, but if we look at two or three rounds McMahon comes out on top. I am looking forward to the next time these guys face off in a tournament, which isn’t until August at the MVP Open on the very challenging Maple Hill course.
I ran a t-test comparing the mean values and the p-value was 0.68, which is well above the cut off value of 0.05 that indicates statistical difference. ↩
The logic can continue here. If an individual pars two holes on a par 90 course they can make them up with two eagles or an albatross, and so on and so forth. ↩
The index equation is: (1-RS/PS)/(1-36/54) = (1-RS/PS)/(1/3) where RS is the round score, and PS is the par score. The denominator is there for scale. It makes a score of 36 on a par 54 hole have an index value of one. Admittedly, the relationship between par and scoring difficulty breaks down at the extremes. For example, it is probably technically easier to have a truly perfect round of all aces at a course that is par 54 than a par 90 course because, presumably, the holes are shorter distances at the par 54 course. Fortunately, a round of all aces or anything close to that is in the realm of the absurd and does not influence the validity of the index. ↩
The scoring distributions are approximately normal, so I am using normal distributions to calculate the probabilities of these round scores. Technically, I am calculating the probabilities of these scores or any lower score. ↩